1.本周学习总结
1.思维导图
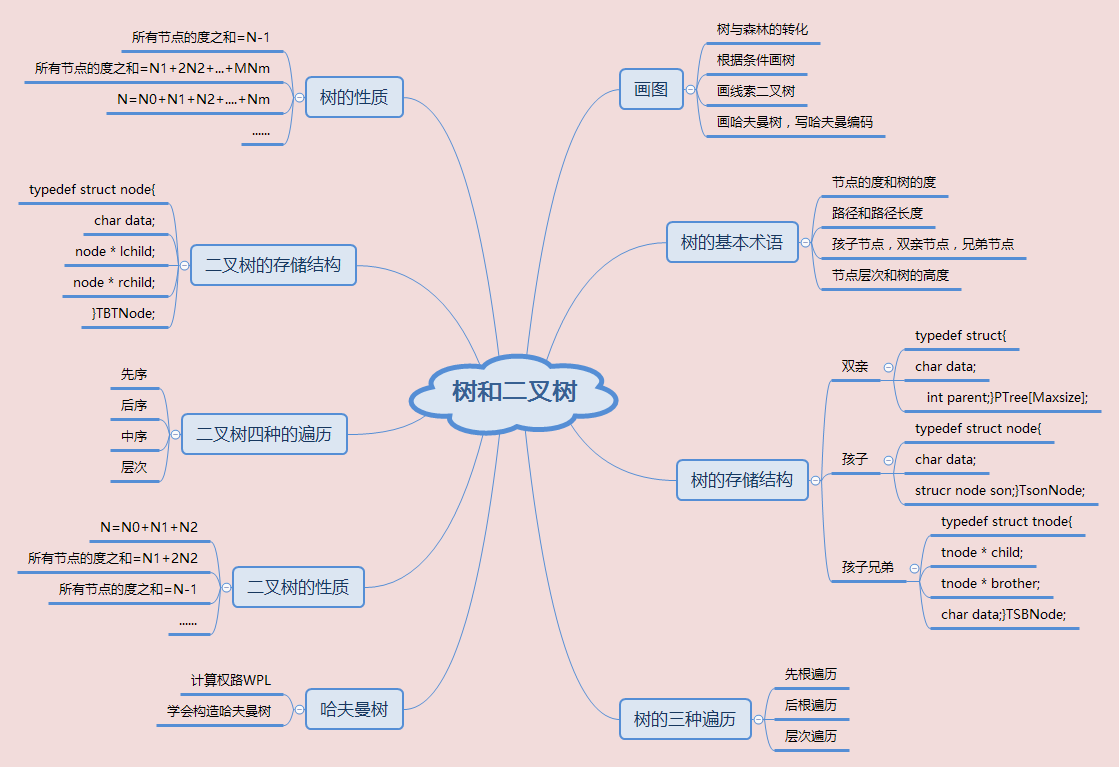
2.谈谈你对树结构的认识及学习体会
- 对于树学到了树的多种存储结构，孩子树，双亲树，孩子兄弟树，二叉树，结构体中的内容差不多都是值和指针的组合，但是也各有个的优缺点，比如孩子树找孩子十分方便找双亲就困难，空指针域也较多比较浪费等。对于树的操作一般从建树开始，然后遍历，遍历又分为多种顺序的遍历，比如二叉树的遍历就有四种，其中先序中序后序遍历可用递归完成，其后就是一些求高度求宽度找路径，插入删除的操作。
关于树的学习，我觉得要记住的内容有点多，树的基本术语，树的性质，好多条没有好记性记了好久一直忘记或记错，还有就是画树的课堂派题目，用画图软件画真的很费时间，一题能画半个小时，最近这两周的时间比较不够选修课有大作业，树有大作业又要复习概率，又有物理实验，几乎没时间写pta ，题目真的写得少，然后不知不觉树学完了。
2.PTA实验作业
2.1.题目1：表达式树
2.1.1设计思路（伪代码）
建表达式的二叉树函数 op.push('#'); while str[i] then if !In(str[i]) then//不是运算符 T=new BTNode; T->data=str[i++]; 左右孩子为空 T入栈 end if else//是运算符 switch Precede(op.top(),str[i])//优先级的比较 case'<': 进栈 case'=': 出栈 case'>': 建一个节点，值为符号栈顶， 左右孩子分别为数据栈顶 T->rchild=digit.top(); digit.pop(); T->lchild=digit.top() digit.pop(); T入栈 end swith end else end while while op.top()!='#' then 同 case'>'的情况 end while T=digit.top();}计算表达式树函数 if !T->rchild&&!T->lchild then//递归口 return T->data-'0'; end if item1=EvaluateExTree(T->lchild); item2同上 switch T->data//运算符的处理 case'+': return item1+item2; break; "-"和"*"同上 case'/': if item2==0 then//分母为0的情况 cout<<"divide 0 error!"; exit(0); end if return item1/item2; break; end swith 2.1.2代码截图
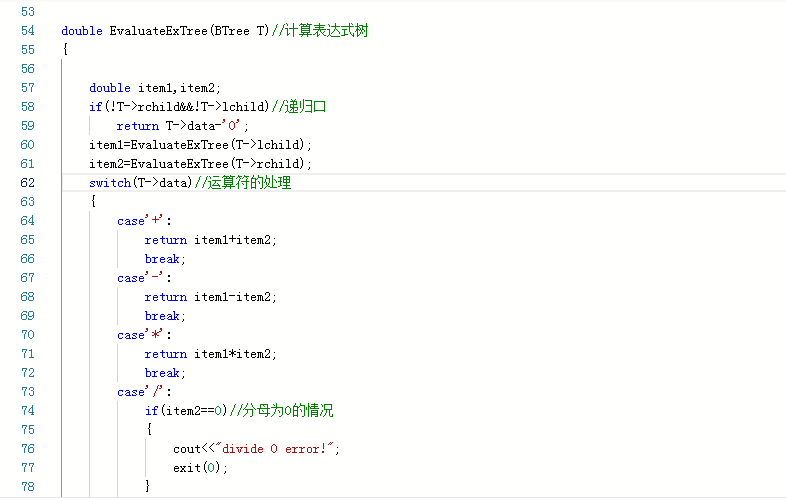
2.1.3本题PTA提交列表说明
问题1：用测试样例试没问题，用自己想的数据没问题，都快怀疑人生了。 解决1：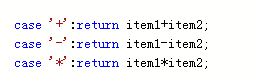
，加break真的很重要。 问题2：一直段错误，改了好久。 解决2：用惯了for循环while循环的时候没有i++,而且还忘了出栈，找了半天问题所在。 2.2.题目2：二叉树叶子结点带权路径长度和
2.2.1设计思路（伪代码）
typedef struct BTNode* BTree;struct BTNode{ char data; BTree lchild; BTree rchild;};建树函数 BTree T; if i大于str的长度-1或str[i]等于#号 then return NULL; end if T=new BTNode; T->data=str[i]; T->lchild=CreateBTree(2*i,str); T->rchild=CreateBTree(2*i+1,str); return T;获得WPL函数 if T==NULL then return; if 左右孩子皆为空 then wpl=wpl+h*(T->data-'0'); h=0; end if h++; GetWpl(T->lchild,wpl,h); GetWpl(T->rchild,wpl,h);主函数 string str; BTree T; int i=1; int wpl=0; int h=0; 输入str T=CreateBTree(i,str); GetWpl(T,wpl,h); 输出wpl return 0; 2.2.2代码截图
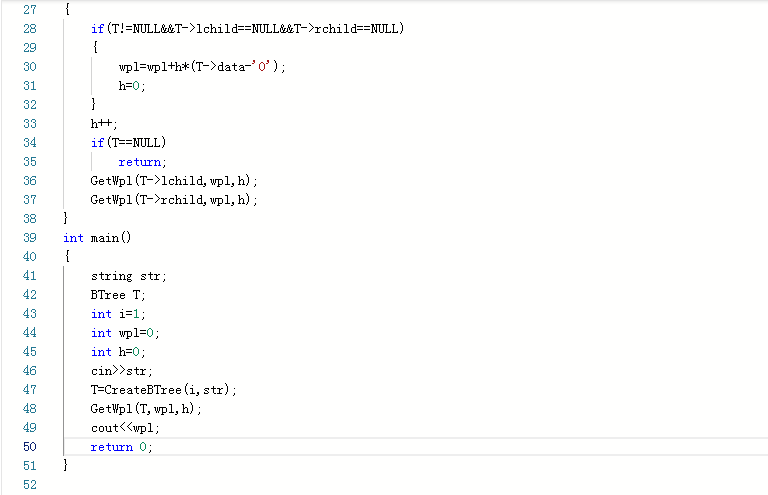
2.2.3本题PTA提交列表说明
2.3.题目3：输出二叉树每层节点
2.3.1设计思路（伪代码）
typedef struct TNode * BinTree;struct TNode{ char Data; BinTree lchild; BinTree rchild;};建树函数 BinTree bt; if i大于str的长度-1或str[i]等于#号 then return NULL; end if bt = new TNode; bt->Data = str[i]; bt->lchild = CreatTree(str, ++i); bt->rchild = CreatTree(str, ++i); return bt;层次遍历函数 queue qt; int level=0; BinTree curNode,lastNode; curNode=lastNode=BT; if BT为空 then cout<<"NULL"; return ; end if else BT入栈 end else while qt非空 if curNode等于lastNode level++; if level==1 then//第一行 cout< <<":"; end if else//其余行 cout< < <<":"; end else lastNode=qt.back(); end if curNode=qt.front(); cout< Data<<",";//格式 if curNode->lchild非空 then qt.push(curNode->lchild); end if curNode->rchild 同上 qt.pop(); end while主函数 char str[100]; BinTree BT; int i=0; cin>>str; BT=CreatTree(str,i); LevelOrder(BT); 2.3.2代码截图
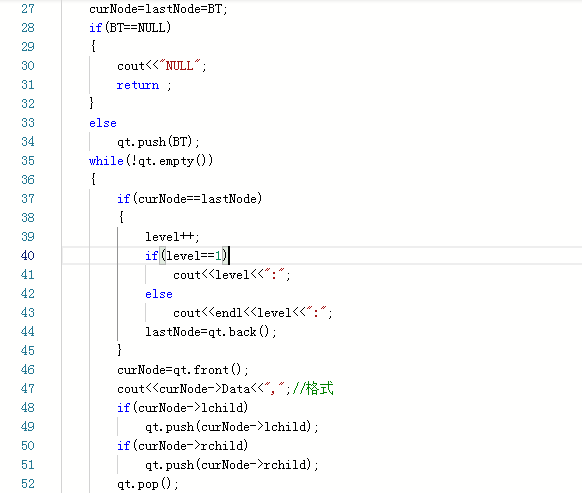
2.3.3本题PTA提交列表说明
3.阅读代码
3.1 题目
给出一棵二叉树，其上每个结点的值都是 0 或 1 。每一条从根到叶的路径都代表一个从最高有效位开始的二进制数。例如，如果路径为 0 -> 1 -> 1 -> 0 -> 1，那么它表示二进制数 01101，也就是 13 。
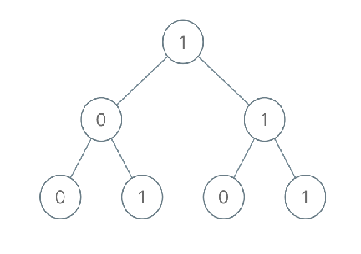
示例：输入：[1,0,1,0,1,0,1]输出：22解释：(100) + (101) + (110) + (111) = 4 + 5 + 6 + 7 = 22
3.2 解题思路
这是一颗二叉树，从根节点开始遍历，每向下一个节点，我们可以把父节点传入的值进一位并加上当前节点的值。这样我们就得到了一个从根节点到当前节点表示的数值。接下来我们要做的只是判断一个节点是不是叶子节点，如果是的话就累加进入sumRootToLeaf函数，返回，否则继续sumRootToLeaf_sub函数。
3.3 代码截图
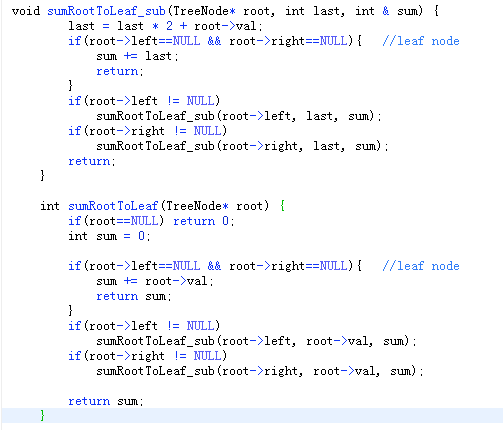
3.4 学习体会
- 这段代码运用了多个递归，在非叶子节点一直运用sumRootToLeaf_sub函数进行计算，效率挺高的，每个节点遍历一次，时间复杂度O(N),不需要额外的存储空间，空间复杂度O(1).其中的代码
last = last * 2 + root->val;其实就是一个左移和或的运算，last = last <<1 | root->val;，乘二再加，比较符合我们学过的转进制的思想；还有在sumRootToLeaf函数里的叶子结点的判断，避免了一个节点无限循环的情况。